Suchen Sie Weihnachtslektüre? Lesen Sie Harry Pauls Physikalische Plaudereien!
komblog
Rund um den Quantensprung...
Samstag, Dezember 24, 2022
Donnerstag, März 17, 2022
Türme von Hanoi
In der Informatik gelten die Türme von Hanoi (Wiki) als ein Paradebeispiel für ein Problem, das sich nur rekursiv (oder iterativ) lösen lässt. Die Zeit für die Berechnung einer bestimmten Position n wächst also exponentiell mit O(2n). In diesem Artikel wird eine explizite Lösung vorgestellt, mit der man jede Position n mit der gleichen Rechenzeit O(1) berechnen kann. Diese explizite Lösung wird in allen Animationen verwendet:
http://mikomma.de/hanoi/hanoi.htm
Sonntag, Juli 11, 2021
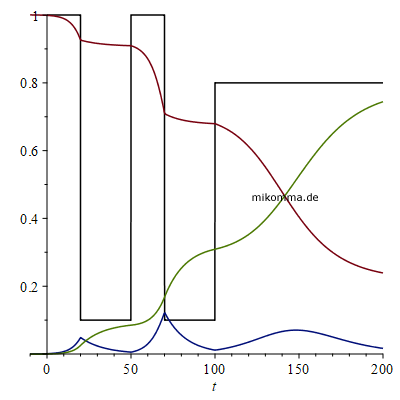
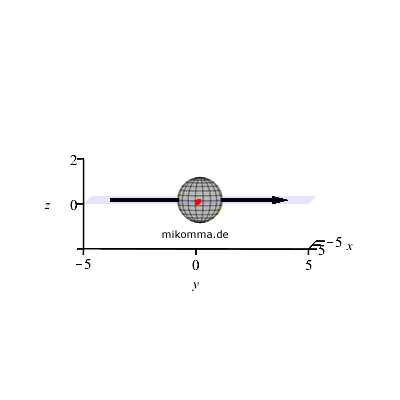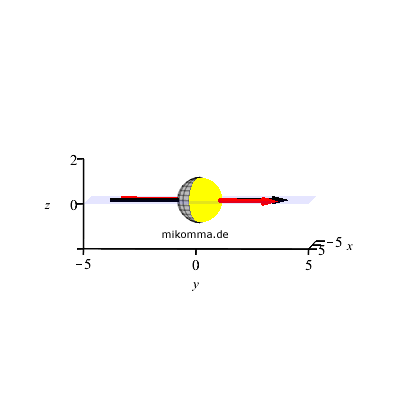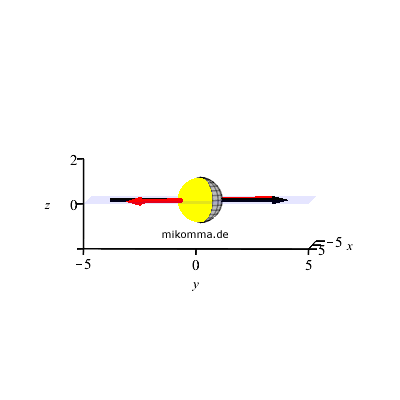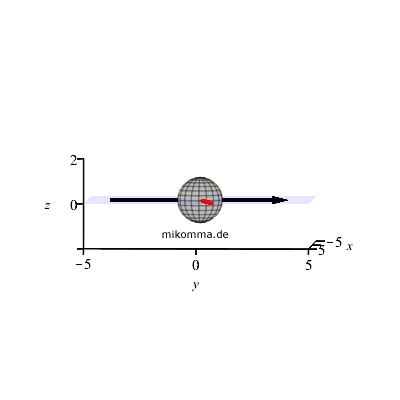
Minev Quantum Jump
To catch and reverse a quantum
jump...
Und die Theorie dazu?
| I think most
physicists, even though they may profess
faithful belief in the Copenhagen interpretation,
still share with me a disreputable,
materialistic prejudice that stones and trees
cannot be either more - or less - real than the
atoms of which they are composed. And, if it is
meaningless to ask what an individual moment is
doing, can it be any more meaningful to ask what
their sum is doing? E.T. Jaynes, Survey of the present status of neoclassical radiation theory. |
Das Zitat von E.T. Jaynes ist vielleicht nicht so bekannt wie Schrödingers "In the first place it is fair to state that we are not experimenting with single particles, any more than we can raise Ichthyosauria in the zoo." (Are There Quantum Jumps? Part I, The British Journal for the Philosophy of Science, 3, (1952), 109-123 [B 12]), und natürlich ist Schrödingers Katze noch bekannter. Dabei geht es immer um das gleiche Problem: beschreibt die Quantentheorie (QT) das Verhalten eines Ensembles oder einzelner Teilchen? Und es schließt sich die Frage an, ob es einen "objektiven Zufall" der QT gibt, oder eine deterministische "Entwicklung des Individuums" (Katze, Saurier oder Atom) kontinuierlich abläuft, oder erst bei einer Beobachtung auf einen Wert "springt". Ganz zu schweigen von der Vielzahl der Interpretationen der QT, mit denen man versucht, diese Widersprüche unter den Teppich zu kehren.
Donnerstag, Oktober 01, 2020
Ensemble - Individuum
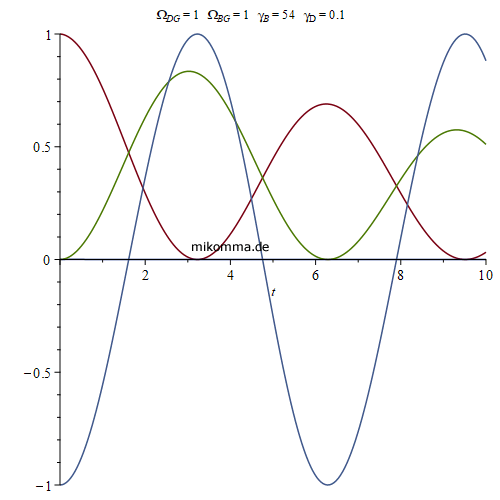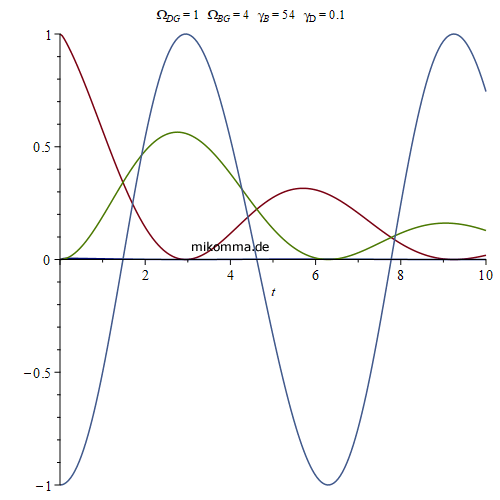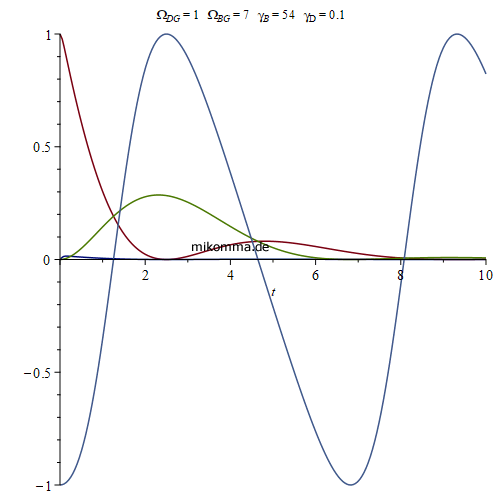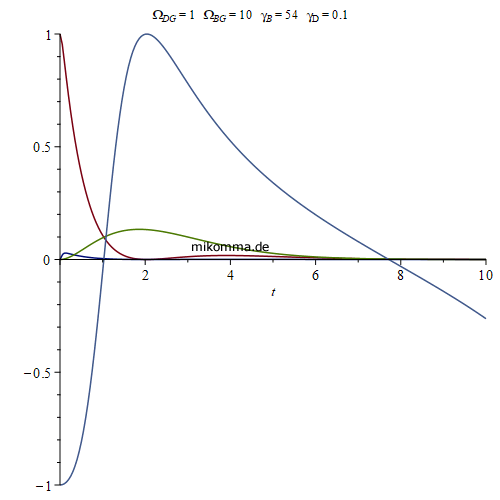
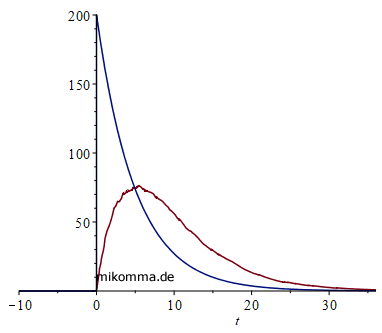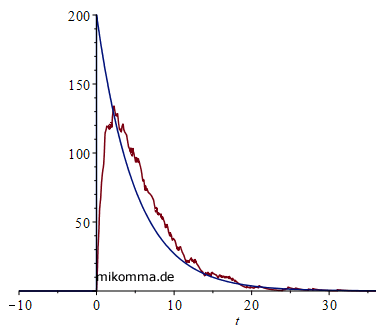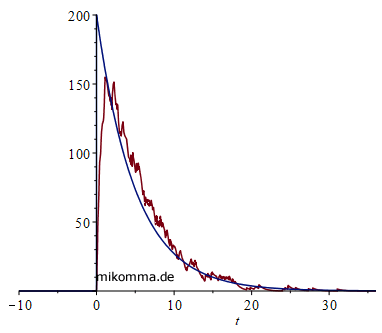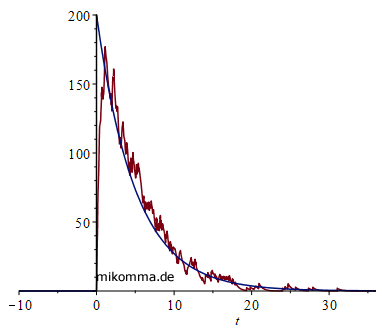
Spontane Emission von Photonen:
90 Jahre mit den falschen Gleichungen?
http://mikomma.de/ensind/ensind.htm